Games of chance: Learn about payout ratio and variance
Principles described in this article can be applied to almost any game of chance in which a player plays against the house. In other words, all games where a casino collects bets and pays out potential winnings. The most famous of such games are slot machines, roulette, blackjack and baccarat, but there are many others.
Most of you probably know that these games are somehow set to give casinos a certain advantage in the long-run. Otherwise, the owners of the casino would be losing money on them. This advantage is also known as a house edge.
The advantage of the casino is determined by the rules of each game and by the payout rules in the case of winning. If these rules are applied over many, many rounds (sometimes even hundreds of thousands of times), casino owners can be quite certain that the sum of bets collected will exceed the total amount of wins payed out. The statistics work in favor of the casino in the long-run.
In spite of long-term statistics working against you, it's quite common to come to a casino, play, win, and leave with your winnings. The main reason is that your visit to a casino consists only of several tens or hundreds of game rounds. In this case, the statistics don't have enough time to converge (show up). The outcome of your casino visit is then more determined by chance (or by your luck, if you want). It's exactly this chance which helps lucky players win and beat the statistical advantage of the casino, although just in the short term.
To increase the chances of "beating the statistics", it's very important to know two basic characteristics of each game – payout ratio and variance. That's exactly what we'll focus on in this article.
Table of contents
Games of chance and payout ratio (RTP)
Payout ratio (also known as expected return, payout percentage or RTP – return to player) of a game of chance is the long-term statistical rate of total money won divided by the total money staked. The opposite of the payout ratio is the house edge. The house edge is calculated as 100% minus payout ratio. If the payout ratio is 95% then the house edge is 100% – 95% = 5%.
Let's take a closer look at payout ratios of some of the most popular games of chance.
Payout ratio of roulette
In European Roulette, the probability of winning when betting on the black color is 18 (# of the black numbers) divided by 37 (# of all numbers, don't forget the zero). The payout is 2 times the bet.
The payout ratio of roulette is then 2 * 18 / 37 = 0.973 = 97.3%. House edge is then 100% – 97.3% = 2.7%. The roulette game is set to have the same RTP for all kinds of bets (color, number, etc.).
Blackjack RTP
As blackjack rules may vary from casino to casino, it's obvious that RTP may differ as well. But generally, a game of blackjack played by a player utilizing the basic blackjack strategy gives an expected RTP of around 99.5%.
In live and online blackjack the expected RTP changes as the dealer deals cards from the deck. The RTP in this case is usually between 95% and 102%, depending on which cards are left in the "shoe". This is exploited by card counters – players which estimate the actual RTP of the blackjack deck and try to bet high if the RTP is over 100%, to make a long-term profit. On the other hand, casinos also have means to detect such card-counters and prevent them from playing further.
Payout percentage of slot machines
The RTP of slots is usually between 92% and 99%. Payout percentage of slot machines is determined by the symbols on the virtual reels, by payout table, and by other specific rules applied to each particular game. If you are curious which slots have the highest RTP, check this Wolfie's collection of best paying slots.
Variance (volatility) of games of chance
To put it simply, the variance (also known as volatility) of a game determines how rapidly your bankroll is changing when you play the game:
- When playing a game with low variance, you win small winnings quite often. In this case, your bankroll changes quite evenly, although, unfortunately, usually downwards.
- In the case of a high-variance game, you lose in a vast majority of rounds, but when you win, you win high. Gradual drop-downs are, from time to time, replaced by a big gain.
Variance of the game can also be described by the statistical distribution of winnings. As they are usually proportional to the bet size, we are talking about the distribution of winnings expressed as a multiple of the bet. When betting on a color in roulette, all winnings are paid out as double of the bet. When betting on a single number, all winnings are paid out as 36-times the bet.
The variance of slots is a bit more complicated. You can hit many various winning combinations and win many different multiples of your bet. Due to this, it's not that simple to describe slot variance by one number, and game providers only use loose descriptions like "small", "medium", and "high" for their slot machines.
Variance of a game has a significant impact on your chance to walk away from a casino as a winner. The rule of thumb is "The higher the variance is, the better":
- The first reason is that in a game with high variance it's easier to win the amount that satisfies you in one game round.
- The second reason is that more rounds end up with a loss and so you don't bet that much from your previous winnings (which has a negative impact on the RTP of your betting system). In other words, you lose more quickly.
- The third reason is that if you can win a higher multiple of the bet, you can bet less to have a chance to win the same amount. This, again, reduces the total sum of your bets and therefore also reduces your long-term losses.
Just to illustrate, let's assume a game with no variance and 99% RTP. In this game, a $1 bet would pay out $0.99. The outcome of each round would be determined and winning in this game would be impossible. Of course, no one would like this game, but it illustrates the fact that a high RTP is not all that matters.
Expected return of a betting system
It's very important to realize that the payout percentage expresses expected payout from a single game round. Let's assume that you bet $100 on roulette and win $1200. Then you continue playing and stake 12 times $100 = $1200. The RTP must be used on each game round separately. The expected statistical casino profit in this case would be ($100 + $1200) * (100% - 97.3 %) = $1300 * 2.7 % = $35.1.
Note that 97.3% is the RTP of European roulette. If you continue playing with your previous winnings, then you should expect to lose more than the previously declared house edge of the game. Most of the players place bets from their previous winnings again and again, losing a portion of their money each time.
If you want to be a smart player, you must distinguish between the RTP of the game (which applies only to a single game round) and the expected return of your betting system.
Your betting system is determined by how you play during your whole stay in a casino or your entire session in an online casino. This includes selection of the game, its variant and settings, sizes of your bets and decisions about when to stop playing.
It's difficult to imagine the RTP of a betting system taking into account just one player. That's why we always run simulations with at least a million of players to get reliable results. The expected return of a betting system can be defined as a ratio of the overall winnings of players who managed to hit their "target", to net losses of players that weren't that lucky.
In reality, if players place bets using their previous winnings, they lose more. The RTP of a poor betting system may drop far below 50%. Even for blackjack – a game with an RTP of 99.5%. As you will see, the RTP of bad betting systems is close to 0%.
The optimal betting system is one which has the same RTP as the game played. To achieve this, you must avoid placing bets using the money you've previously won. Theoretically, the easiest way to achieve this is to stake your whole budget in one round. Then keep betting all-in until you lose or win a satisfactory amount of money. Roulette is a very good game for this system as you can choose the odds of your bet.
Let's assume that you have $100 to play with and ending up with $900 will satisfy you. Placing $100 on a square (4 numbers) is almost the optimal strategy in this case. You will either leave the casino with a nice amount of money or without $100, but your chances are quite fair. The biggest disadvantage of this approach is that you will play only for a very short period of time.
How variance of the game influences the expected return of the betting system
Now we will demonstrate one very simple betting system. Note how the variance of the game affects the expected return of the betting system. Imagine two players, each of which came to a casino with $100.
- Player X bets $10 on a number in roulette.
- Player Y places bets on color.
Each of them leaves the casino if their bankroll exceeds $500 or if they lose all their money. We have simulated both players one million times, using a simple software routine with a random number generator.
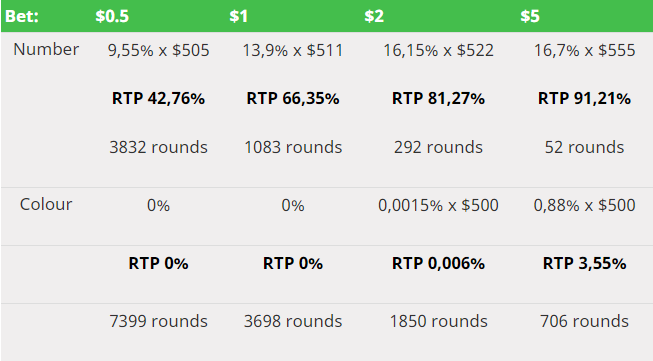
Player X left the casino as a winner in 14.8 % of his attempts. His average "winning" bankroll was $648 and he played 16 rounds in average. This means that the RTP of his betting system was 95.19 %.
Player Y managed to win in only 5.15% of his attempts. His system had an average "winning" bankroll of $500 and an overall RTP of 21.42%. On the other hand, player Y enjoyed playing for a much longer time – in average 274 rounds.
From this example you can clearly see that variance of the game significantly affects your chances to leave the casino as a winner. The payout ratio of player X's system was 4.4 times higher than the RTP of the system used by player Y.
How bet size affects the RTP of a betting system
Win amounts in games of chance are usually calculated using the bet size. The overall payout ratio of your betting system is therefore also affected by the size of your bets. The rule of thumb is simple: The higher the size of your bets, the higher (usually) the RTP of your betting system. We assume that all the other rules and parameters of the betting system, including the initial bankroll, remain the same.
We will again use roulette to demonstrate the effect of the bet size on a betting system's results. The players again come to a casino with $100 and leave if their bankroll reaches 0 or exceeds $500. Player X bets $20 and player Y bets $5 in each game round. Both players place bets on color (red or black).
- After simulating one million instances of player X, we found out that 10.9 % of them managed to get to $500. This amounts to a 48.68% RTP and an average of 84 rounds played.
- On the other hand, out of one million instances of player Y, only 0.88% managed to win (an average of 706 rounds, RTP of 3.55%). If player Y wants to leave the casino with $500, he must win 80 game rounds more than he loses. It seems that having such a "run" on roulette is quite rare.
The statistics are clear in this case. When placing low bets on a low variance game, you may be playing for longer, but your odds to win a satisfactory amount of money drop significantly.
On the opposite side of the variance spectrum is a combination of a high variance game with high bets. Player Z came to a casino with $100 and he decided to play all-in on roulette on a single number. The results of simulation show that from one million Z players, only 2.71% managed to win. However, each of the winners left with $3600 (RTP of 97.4%). Each of the Z players played exactly one round.
The recommended roulette betting system
A good betting system is therefore a tradeoff between odds of a satisfactory win and its size, and duration of your stay in a casino.
Which betting system should you choose if you wish to play for a reasonable amount of time while having a good chance of winning? The following table shows the results of our simulations. The variables are the size of a single bet and bet type (color/number). Each player begins with $100 and leaves the casino with $500 or more (or after losing everything).
The table contains the portion of players which managed to win, the average size of their win, the calculated RTP of such a betting system, and the average number of rounds played.
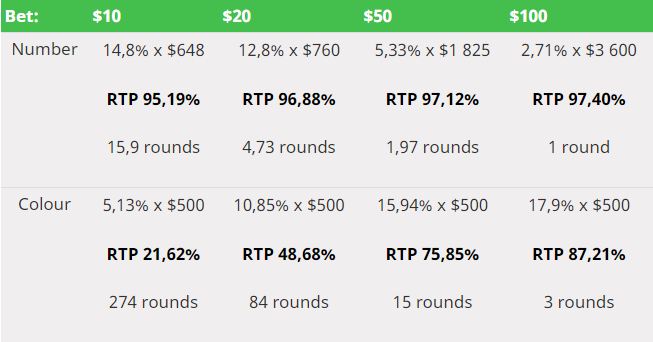
As you can see, a much higher variance of bets on a number can easily beat bets on color which are significantly larger in size. In addition, your stay in the casino will take much longer. Also note that when betting $2 on color, your chances to get to $500 are close to 0. None of the one million attempts were successful in this case.
If your goal is to have fun and have good odds of winning, we recommend you choose a game with the highest possible variance and play it with adequately small bets.
In the case of roulette and a $100 budget, betting $2 – $4 on your lucky number seems to be one of the best options with a fixed bet type and bet size.
Conclusions
Here are the most important things to take away from this article:
- Payout percentage of games of chance applies only when considering a single game round. Your real expected return will be lower due to re-betting previous winnings.
- You statistically lose on every bet. A fewer bets means a smaller statistical profit for the casino.
- The RTP of your betting system depends on the RTP of the game, variance of the game, size of your bets, and rules when to leave and when to keep playing.
- Variance of the game is determined by the size of potential winnings as multiples of the bet. The higher the individual wins, the higher the variance of the game (considering a fixed RTP).
- Games with high variance are usually more favorable. The advantage of significantly higher variance can easily beat the advantage of slightly higher RTP.
- The higher the variance, the higher the chance of turning small sums of money into huge sums of money.
- The bigger the bets in one round, the higher the RTP of your betting system, considering a fixed bankroll.
- If you play for fun, look for games with high variance and place smaller bets. A few wins could get you to your desired win, otherwise you will lose your whole budget. Keep in mind that you are doing a tradeoff between the duration of your play and the RTP of your betting system.