Why Odds Matter: University Professor Explains The Mathematics of Roulette.

About the author: Mark Bollman is Professor of Mathematics at Albion College in Albion, Michigan, USA. He is the author of 4 books on gambling mathematics published by CRC Press/Taylor & Francis; the most recent is Mathematics of the Big Four Casino Table Games. Mark has taught 118 different courses, at 6 colleges, in his career. He and his students have traveled to casinos in Michigan and Nevada to explore the connections between theory and practice as they play out on the casino floor.
How do casinos make their money?
It’s very simple: the rules of every casino game are set to guarantee the house a long-term advantage. All that a casino has to do is open for business and offer games using "standard" rules. There may be short-term fluctuations, and some gamblers with a bit of luck and the strength to walk away when they’re ahead may leave with more money than they came in with, but in the long run, the house will always get its proper percentage of the total amount wagered.
The house edge of a casino game is typically expressed as a percentage of the total wager, as we will explain below. If a casino sees $10,000 in action on a game with a 4% advantage, an average day will see $400 in wagers retained by the house after all winning bets have been paid. Depending on the game, calculating this advantage may be a matter of simple arithmetic or may require intricate calculations or computer simulations. One simple rule that might guide us was quoted in the "Luck Be An Old Lady" episode of the TV series Sex and the City:
The easier a bet is to understand, the greater the house edge.
For example, the house edge on state lottery draw games, such as Powerball, frequently exceeds 50%. Blackjack and baccarat, which are more complicated games, have house advantages near 1%, and make money for casinos by high wagering volume: a casino taking $10,000,000 in baccarat bets is nearly always going to retain about $100,000.
Roulette is instantly recognizable as a glamorous casino game and certainly qualifies as easy to understand: there is no strategy involved when playing the game: simply make your wager and hope that a number on which you’ve bet turns up. A large wheel is spun on a vertical axis; a small ball is released onto the spinning wheel and eventually settles in one of a number of labeled pockets along the wheel’s outer rim. Gamblers may make a variety of bets as they attempt to predict where the ball will come to rest.
An American roulette wheel is divided into 38 pockets, and is shown here.

The pockets are numbered from 1–36, 0, and 00. The 0 and 00 pockets are colored green; the other numbers are colored red or black.
The American roulette layout, where wagers are placed, is shown here.

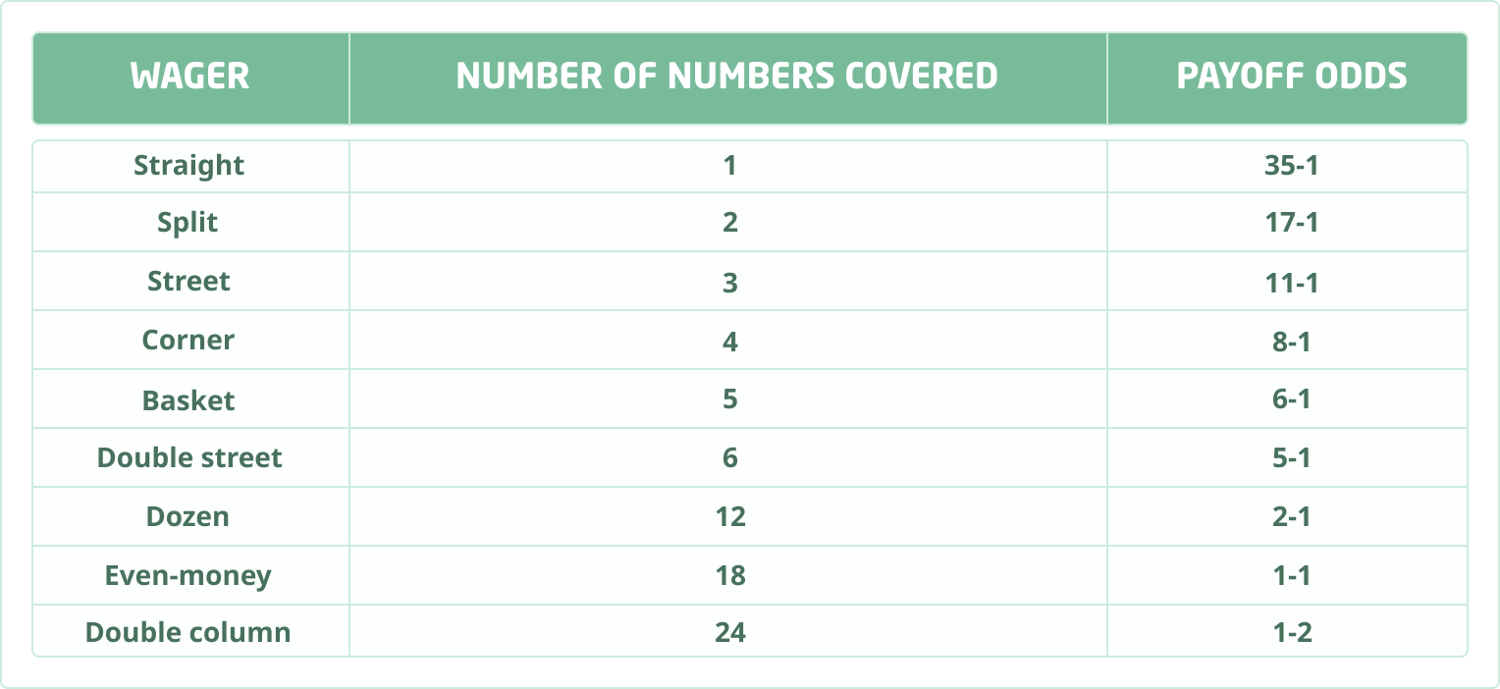
The following wagers are available to players:
| Wager | Number of Numbers Covered | Payoff Odds |
|---|---|---|
| Straight | 1 | 35-1 |
| Split | 2 | 17-1 |
| Street | 3 | 11-1 |
| Corner | 4 | 8-1 |
| Basket | 5 | 6-1 |
| Double street | 6 | 5-1 |
| Dozen | 12 | 2-1 |
| Even-money | 18 | 1-1 |
| Double column | 24 | 1-2 |
With the exception of the basket bet, a bet on n numbers pays off at\((36-n)/n\)to 1. The winning player’s original wager is returned with the payoff.
This formula allows for easy calculation of the casino’s advantage on all of these bets. The expected value of a casino wager is found by computing the probability of each possible outcome, multiplying each probability by the value of the outcome, and adding all of the products together. For example, if we consider a 1-unit bet on the number 33, there are two possible outcomes:
The expected value of this bet is then\(E = (35) * 1/38 + (-1) * 37/38 = -2/38 ≈ -.0526\).
This means that an "average" outcome for this bet is the loss of 5.26 betting units. (The value of a unit is determined by the player; it could be $1, $5, ^1, €5, or any amount the gambler wishes to risk. For convenience, we will usually consider 1-unit wagers.) Expected values of casino wagers are almost always negative; this represents the fact that the games are designed so that the casino wins money in the long run.
The house advantage (HA) of a bet of N units where the expected value is E is then defined to be\(HA = -E/N\), which is frequently expressed as a percentage. The wager above has a HA of .0526, or 5.26%. In the long run, the casino will retain 5.26% of all money wagered on single-number bets.
This extends to every other bet except the basket bet. A bet on n numbers has win probability n/38 and pays off (36-n)/n when it wins, so the house advantage is\(E = ((36-n)/n) * n/38 + (-1) * (38-n)/38 = (36-n-38+n)/38 = -2/38\), which is independent of n. Any wager at American roulette, other than the basket bet, has a constant HA of 5.26%.
The basket bet is worse. The payoff formula (36-n)/n for a bet on n numbers yields 6.2 when n = 5. This is rounded down to 6–1, so the corresponding expectation is\(E = (6) * 5/38 + (-1) * 33/38 = -3/38 ≈ -.0789\), and the house edge is 7.89%.
There is no real strategy for American roulette, other than "don’t ever make the basket bet". Every other bet on the layout is equally bad, holding the same 5.26% edge for the casino.
European roulette wheels have only a single 0. The payoff odds remain the same, but the denominators in the probability calculations change from 38 to 37. Every bet on a European wheel has an expected value of\(E = ((36-n)/n) * n/37 + (-1) * (37-n)/37 = -1/37 ≈ -.0270\), so the house edge drops from 5.26% to 2.70%.
Many European wheels make the even-money bets more attractive by invoking the "en prison" rule. Under this rule, even-money bets do not automatically lose when 0 is spun. Rather, they are held "in prison" for one additional spin. If that spin results in a win, the player’s original wager is returned, though no winnings are paid. If the second spin loses, including if a second 0 is spun, the bet loses.
There are thus 3 outcomes to a 1-unit even-money bet:
The expected value is then –.0139 units, giving the house a low HA of 1.39%. If you’re going to play European roulette, the mathematically best strategy is to restrict your bets to the even money bets at a table with the en prison option.
In 2017, the Venetian Casino in Las Vegas introduced Sands Roulette. This game added a 39th pocket to an American roulette wheel, which was colored green and bore an "S" for Sands, the parent company of the Venetian. The S space acts like a third zero for betting and payoff purposes. It is represented on the layout by a rectangle above the 0 and 00 spaces, so it also belongs to no column. Basket bets are available on this layout. The following year, 000 spaces appeared on some roulette wheels along the Strip, at New York–New York and Planet Hollywood, and the Luxor added a 39th pocket bearing its pyramid logo. The payoffs remain the same: (36-n)/n except for the basket bet, but the probability of winning drops and so the HA rises.
The expectation of a 1-unit bet, other than the basket bet, at Sands Roulette, is\(E = ((36-n)/n) * n/39 + (-1) * (39-n)/39 = -3/39 ≈ -.0769\).
The house holds an advantage of 7.69%.
It’s easy to see why a casino would offer this option – a higher HA means more money retained from gamblers – but why would players choose it? Some gamblers might think that more numbers means more chances to win. A more plausible reason is that some casinos offer lower minimum bet limits at triple-zero tables. For example, a casino might choose to impose a $10 minimum at a triple-zero table but raise the minimum to $25 on an American or European wheel. Gaming statistics suggest that players are not deterred from gambling by the third zero.
While we wait for some enterprising casino to add a 4th zero, we can compute its effect in advance and consider a general formula. Let z be the number of zeroes on a roulette wheel, so z = 1 for European roulette, z = 2 for American roulette, and z = 3 for Sands Roulette. The expected value of a 1-unit bet on n numbers, n *5, assuming that the payoffs are not changed, is then\(E = ((36-n)/n) * n/(36+z) + (-1) * (36+z-n)/36+z = -z/(36+z)\).
In addition to confirming the results above for American, European, and Sands roulette, we can calculate that a wheel with 000 and 0000 pockets would offer casinos a 10% advantage.
There are other ways to manipulate roulette to change the HA, either to raise it in the casinos’ service or lower it to attract more players. An electronic American roulette machine at the Rivers Casino in Illinois reduced some of the payoffs. Payoffs for corner, basket, double street, and even-money bets were unchanged, but a single-number bet paid only 32 for 1, where the use of "for 1" instead of "to 1" means that the player’s original bet is returned as part of the payoff, not in addition to it. The effective payoff on this machine was then 31–1. This bet carried a 15.79% house advantage—triple the edge of a single-number bet on a live game. The same increased HA applied to the split bet, which paid 15–1, and on the street bet where the payoff was reduced to 10–1.
Some gamblers prefer electronic versions of table games because they’re intimidated by the crowd or seek out lower-limit games. If the payoffs on the electronic games match the live payoffs, there is no difference, but if the payoffs change like in this example, the price of intimidation can be considerable. In addition to "don’t make the basket bet", a gambler considering an electronic roulette machine would be well-advised also to "check the pay table and make sure that you’re getting standard payoffs – and be careful about the difference between ‘to 1' and ‘for 1'."


Send us a tip
RECOMMENDED TOPICS
gambling industryresponsible gamblingappointmentssports bettinggambling lawslotterycasino
















